- Bisection Method Fortran
- Bisection Method Algorithm Fortran
- Bisection Method Fortran Overriding
- Bisection Method Fortran Programming
BRENT, a FORTRAN90 code which contains algorithms for finding zeros or minima of a scalar function of a scalar variable, by Richard Brent.
The methods do not require the use of derivatives, and do not assume that the function is differentiable.
Licensing:
The computer code and data files described and made available on this web page are distributed under the GNU LGPL license.
Languages:
BRENT is available in a C version and a C++ version and a FORTRAN90 version and a MATLAB version and a Python version.
Related Data and Programs:
ASA047, a FORTRAN90 code which minimizes a scalar function of several variables using the Nelder-Mead algorithm.
The Newton-Raphson Method is often much faster than the Bisection Method. In the last example, we started with an interval of length 1. After 10 steps, the interval a 10, b 10 has length 1/1024. Consequently every 10 steps of the Bisection Method will give us about 3 digits more accuracy - that is rather slow. We first consider the Bisection (Binary search) Method which is based on the Intermediate Value Theorem (IVT). Program For Bisection Method In Fortran; Bisection method is used to find the real roots of a nonlinear equation. The process is based on the ‘‘. According to the theorem “If a function f(x)=0 is continuous in an interval (a,b), such that f(a) and f(b) are of opposite nature. PROGRAMS WRITTEN IN FORTRAN PROGRAMMING LANGUAGE 1. Finding the roots of an equation using BISECTION method. Finding the roots of an equation using NEWTON'S method. Finding the roots of an equation using SECANT method. Finding the roots of a system of equations using NEWTON'S method. The most basic problem in Numerical Analysis (methods) is the root-finding problem. For a given function f(x), the process of finding the root involves finding the value of x for which f(x) = 0.If the function equals zero, x is the root of the function. A root of the equation f(x) = 0 is also called a zero of the function f(x). The Bisection Method, also called the interval halving method.
BISECTION_INTEGER, a FORTRAN90 code which seeks an integer solution to the equation F(X)=0, using bisection within a user-supplied change of sign interval [A,B].
BISECTION_RC, a FORTRAN90 code which seeks a solution to the equation F(X)=0 using bisection within a user-supplied change of sign interval [A,B]. The procedure is written using reverse communication.
COMPASS_SEARCH, a FORTRAN90 code which seeks the minimizer of a scalar function of several variables using compass search, a direct search algorithm that does not use derivatives.
NELDER_MEAD, a MATLAB program which minimizes a scalar function of several variables using the Nelder-Mead algorithm.
NMS, a FORTRAN90 code which includes versions of Brent's minimizer and zero finder.
PRAXIS, a FORTRAN90 code which minimizes a scalar function of several variables.
SLATEC, a FORTRAN90 code which includes the zero finder FZERO.
TEST_OPT, a FORTRAN90 code which defines test problems requiring the minimization of a scalar function of several variables.
TEST_OPTIMIZATION, a FORTRAN90 code which defines test problems for the minimization of a scalar function of several variables, as described by Molga and Smutnicki.
TEST_ZERO, a FORTRAN90 code which defines some test functions for which zeroes can be sought.
TOMS178, a FORTRAN90 code which optimizes a scalar functional of multiple variables using the Hooke-Jeeves method.
ZERO_RC, a FORTRAN90 code which seeks solutions of a scalar nonlinear equation f(x) = 0, or a system of nonlinear equations, using reverse communication.
ZOOMIN, a FORTRAN90 code which includes various zero finder routines.
Author:
Original FORTRAN77 version by Richard Brent; FORTRAN90 version by John Burkardt.
Reference:
- Richard Brent,
Algorithms for Minimization without Derivatives,
Dover, 2002,
ISBN: 0-486-41998-3,
LC: QA402.5.B74.
Source Code:
- brent.f90, the source code.
The most basic problem in Numerical Analysis (methods) is the root-finding problem.
For a given function f(x), the process of finding the root involves finding the value of x for which f(x) = 0. If the function equals zero, x is the root of the function.
A root of the equation f(x) = 0 is also called a zero of the function f(x).
Bisection Method Fortran
The Bisection Method, also called the interval halving method, the binary search method, or the dichotomy method. is based on the Bolzano’s theorem for continuous functions.
Theorem (Bolzano): If a function f(x) is continuous on an interval [a, b] and f(a)·f(b) < 0, then a value c ∈ (a, b) exist for which f(c) = 0.
Image: Example of a continuous functionA function is continuous when small changes of the argument gives also in small changes in the result. In other words, if x changes with small steps f(x) will also change with small steps, it doesn’t give big “jumps” of the result.

f(a)·f(b) < 0 means that f(a) and f(b) have different signs, which means that one of them is above the x-axis and the other one below the x-axis. In this case, if we plot the f(x) function, at some point, it will cross the x-axis. The x value for which the plot is crossing the x-axis is the root of the equation f(x) = 0.
The Bisection Method looks to find the value c for which the plot of the function f crosses the x-axis. The c value is in this case is an approximation of the root of the function f(x). How close the value of c gets to the real root depends on the value of the tolerance we set for the algorithm.
Image: The Bisection Method explainedFor a given function f(x),the Bisection Method algorithm works as follows:
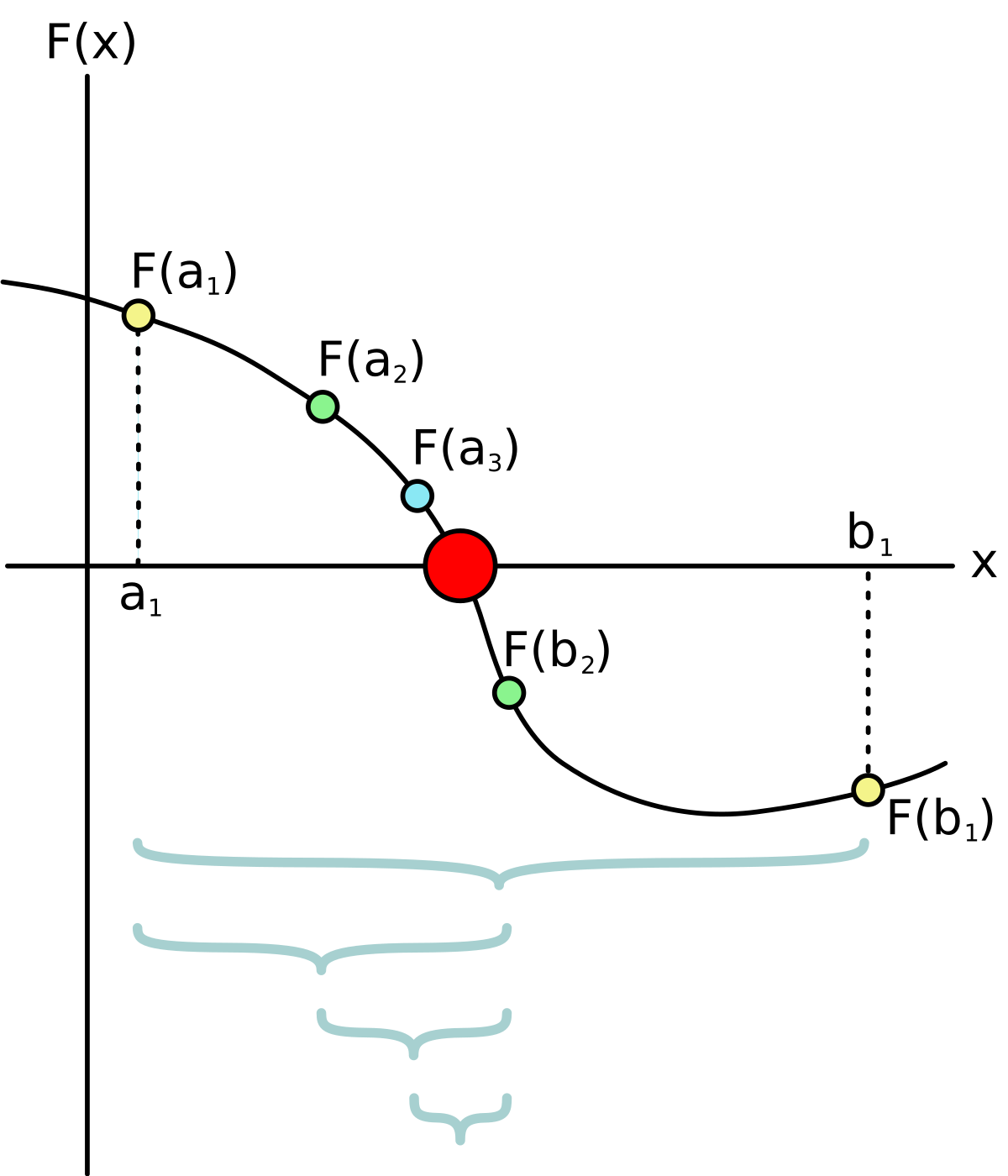
- two values a and b are chosen for which f(a) > 0 and f(b) < 0 (or the other way around)
- interval halving: a midpoint c is calculated as the arithmetic mean between a and b, c = (a + b) / 2
- the function f is evaluated for the value of c
- if f(c) = 0 means that we found the root of the function, which is c
- if f(c) ≠ 0 we check the sign of f(c):
- if f(c) has the same sign as f(a) we replace a with c and we keep the same value for b
- if f(c) has the same sign as f(b), we replace b with c and we keep the same value for a
- we go back to step 2. and recalculate c with the new value of a or b
The algorithm ends when the values of f(c) is less than a defined tolerance (e.g. 0.001). In this case we say that c is close enough to be the root of the function for which f(c) ~= 0.
In order to avoid too many iterations, we can set a maximum number of iterations (e.g. 1000) and even if we are above the defined tolerance, we keep the last value of c as the root of our function.
Image: The Bisection Method Explained as a Logic DiagramThe best way of understanding how the algorithm work is by looking at an example.
For the function f(x) below find the best approximation of the root given the tolerance of TOL = 0.01 and a maximum of NMAX = 1000 iterations.
[f(x) = 10 – x^2 ]In the table below we are going to calculate the values described in the logic diagram above:
| i | a | b | c | f(a) | f(b) | f(c) |
| 0 | -2 | 5 | 1.5 | 6 | -15 | 7.75 |
| 1 | 1.5 | 5 | 3.25 | 7.75 | -15 | -0.5625 |
| 2 | 1.5 | 3.25 | 2.375 | 7.75 | -0.5625 | 4.359375 |
| 3 | 2.375 | 3.25 | 2.8125 | 4.359375 | -0.5625 | 2.0898438 |
| 4 | 2.8125 | 3.25 | 3.03125 | 2.0898438 | -0.5625 | 0.8115234 |
| 5 | 3.03125 | 3.25 | 3.140625 | 0.8115234 | -0.5625 | 0.1364746 |
| 6 | 3.140625 | 3.25 | 3.1953125 | 0.1364746 | -0.5625 | -0.2100220 |
| 7 | 3.140625 | 3.1953125 | 3.1679688 | 0.1364746 | -0.2100220 | -0.0360260 |
| 8 | 3.140625 | 3.1679688 | 3.1542969 | 0.1364746 | -0.0360260 | 0.0504112 |
| 9 | 3.1542969 | 3.1679688 | 3.1611328 | 0.0504112 | -0.0360260 | 0.0072393 |
At initialization (i = 0) we choose a = -2 and b = 5. After evaluating the function in both points we can see that f(a) is positive while f(b) is negative. This means that between these points, the plot of the function will cross the x-axis in a particular point, which is the root we need to find.
After 9 iterations the value of f(c) is less than our defined tolerance (0.0072393 < 0.01). This means that the value that approximates best the root of the function f is the last value of c = 3.1611328.
We can check our result by solving our quadratic equations in a classic way:
[ begin{equation*} begin{split}10 – x^2 &= 0
x^2 &= 10
x &= sqrt{10} = pm 3.16227766
end{split} end{equation*} ]
Below you can see an animation of the f(x) plot for every iteration. Notice how the [a, b] interval (red horizontal line) is halved at each iteration, until it’s converging into a point where the plot is crossing the x-axis (value of x in that point being the root of the function f).
Image: The Bisection Method animationfor f(x) = 10 – x2
Bisection Method Algorithm Fortran
The example calculated in the table is also executed in the C code below. The results are the same as those calculated in the table. Use this C code (copy and past to into a *.c file and execute) to examine the impact of tolerance (e.g 0.0001) on the number of iterations necessary to converge to a solution.
The same algorithm is implemented in a Scilab script. Play with the a, b, TOL and NMAX parameters to understand their impact on the method.
As you can see, the Bisection Method converges to a solution which depends on the tolerance and number of iteration the algorithm performs. There is a dependency between the tolerance and number of iterations. For a particular tolerance we can calculate how many iterations n we need to perform.
Every iteration the algorithm generates a series of intervals [an, bn] which is half of the previous one:
[b_n – a_n = frac{b-a}{2^n} =|c-x| tag{1}]The tolerance ε is the absolute value of the difference between the actual root of the function x and the approximation c.
[varepsilon=|c-x| tag{2}]For the algorithm to converge within an absolute error tolerance (ε), we need to have:
[|c-x| le varepsilon tag{3}]By replacing inequality (3) with equation (1), we get:
[frac{b-a}{2^n}le varepsilon tag{4}]Solving inequality (4), we obtain:
[2^n ge frac{b-a}{varepsilon} tag{5}]We apply the logarithm function to both sides of the inequality (5):
[log(2^n) ge logleft (frac{b-a}{varepsilon} right ) tag{6}]Solving (6), we get:
[ begin{equation*} begin{split}n cdot log(2) &ge logleft (frac{b-a}{varepsilon} right )
n &ge frac{logleft (frac{b-a}{varepsilon} right )}{log(2)}
Bisection Method Fortran Overriding
end{split} end{equation*} ]From the above result we can understand that, using the Bisection Method, in order to calculate an approximate root of a function within tolerance ε, the number n of iterations we need to perform is:
[ begin{equation} begin{split}bbox[#FFFF9D]{n ge frac{logleft (frac{b-a}{varepsilon}right )}{log(2)}}
end{split} end{equation} ]
For the example presented in this tutorial our algorithm performed 9 iterations until it found the solution within the imposed tolerance. Let’s apply the above formula to see what is the minimum calculated number of iterations.
[ begin{equation*} begin{split}a &= -2
b &= 5
varepsilon &= 0.01
n &ge frac{logleft (frac{5+2}{0.01} right )}{log(2)}
n &ge 9.45
end{split} end{equation*} ]
The result shown that we need at least 9 iterations (the integer of 9.45) to converge the solution within the predefined tolerance, which is exactly how many iterations our algorithm performed.
The Bisection Method is a simple root finding method, easy to implement and very robust. The disadvantages of this method is that it’s relatively slow. Because of this, most of the time, the bisection method is used as a starting point to obtain a rough value of the solution which is used later as a starting point for more rapidly converging methods.
The Bisection Method is summarized in the poster below:
Image: The Bisection Method Explained Poster (click on it for higher resolution)Test your knowledge in the Bisection Method by taking the quiz below:
QUIZ! (click to open)For any questions or observations regarding this tutorial please use the comment form below.
Don’t forget to Like, Share and Subscribe!
Next Article2 Comments
lonz
nice in depth
mahmoudali ali
Bisection Method Fortran Programming
very useful information
Leave a Reply
